向量值函数在机器学习、计算机图形学和计算机视觉算法中经常出现。它们对于定义空间曲线的参数方程特别有用。掌握向量值函数的基本概念对于理解更复杂的概念至关重要。
在本教程中，您将了解向量值函数是什么，如何定义它们以及一些示例。
完成本教程后，您将了解：
- 向量值函数的定义
- 向量值函数的导数
让我们开始吧。
向量值函数的简明介绍。图片由 Noreen Saeed 拍摄，部分权利保留
教程概述
本教程分为两部分；它们是
- 向量值函数的定义和示例
- 向量值函数的微分
向量值函数的定义
向量值函数也称为向量函数。它是一个具有以下两个特性的函数：
- 定义域是实数集
- 值域是向量集
因此，向量函数只是标量函数的扩展，其中定义域和值域都是实数集。
在本教程中，我们将考虑值域为二维或三维向量集的向量函数。因此，此类函数可用于定义空间中的点集。
给定单位向量 i, j, k 分别平行于 x, y, z 轴，我们可以将三维向量值函数写为
r(t) = x(t)i + y(t)j + z(t)k
它也可以写成
r(t) = <x(t), y(t), z(t)>
以上两种表示法是等效的，并且经常在各种教科书中用到。
空间曲线和参数方程
我们在上一节中定义了一个向量函数 r(t)。对于 t 的不同值，我们得到相应的 (x,y,z) 坐标，由函数 x(t), y(t) 和 z(t) 定义。因此，生成的点集 (x,y,z) 定义了一条称为空间曲线 C 的曲线。x(t), y(t) 和 z(t) 的方程也称为曲线 C 的 参数方程。
向量函数的示例
本节展示了一些定义空间曲线的向量值函数的示例。所有示例也绘制在示例后的图中。
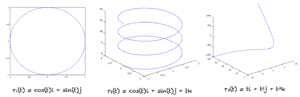
1.1 圆
让我们从二维空间中向量函数的简单示例开始
r_1(t) = cos(t)i + sin(t)j
这里的参数方程是
x(t) = cos(t)
y(t) = sin(t)
由 参数方程定义的空间曲线是二维空间中的一个圆，如图所示。如果我们从 -???? 变化 t 到 ????，我们将生成位于圆上的所有点。
1.2 螺旋线
我们可以扩展示例 1.1 中的 r_1(t) 函数，轻松生成三维空间中的螺旋线。我们只需要添加沿 z 轴随 t 变化的量。因此，我们有以下函数
r_2(t) = cos(t)i + sin(t)j + tk
1.3 扭曲三次曲线
我们还可以定义一条称为扭曲三次曲线的曲线，它具有有趣的形状，如下所示：
r_3(t) = ti + t^2j + t^3k
参数曲线
想开始学习机器学习微积分吗？
立即参加我为期7天的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
向量函数的导数
我们可以轻松地将标量函数的导数概念扩展到向量函数的导数。由于向量函数的值域是向量集，其导数也是一个向量。
如果
r(t) = x(t)i + y(t)j + z(t)k
那么 r(t) 的导数由 r'(t) 计算得到，计算方法如下：
r'(t) = x'(t)i + y'(t)i + z'(t)k
向量函数导数的示例
我们可以计算上一示例中定义的函数的导数，如下所示：
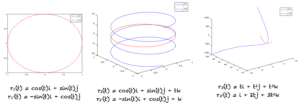
2.1 圆
二维圆的参数方程为
r_1(t) = cos(t)i + sin(t)j
因此，其导数是通过计算 x(t) 和 y(t) 的相应导数来计算的，如下所示：
x'(t) = -sin(t)
y'(t) = cos(t)
这给我们带来了
r_1′(t) = x'(t)i + y'(t)j
r_1′(t) = -sin(t)i + cos(t)j
由参数方程定义的空间曲线是二维空间中的一个圆，如图所示。如果我们从 -???? 变化 t 到 π，我们将生成位于圆上的所有点。
2.2 螺旋线
与前面的示例类似，我们可以计算 r_2(t) 的导数，如下所示：
r_2(t) = cos(t)i + sin(t)j + tk
r_2′(t) = -sin(t)i + cos(t)j + k
2.3 扭曲三次曲线
r_3(t) 的导数由下式给出：
r_3(t) = ti + t^2j + t^3k
r_3′(t) = i + 2tj + 3t^2k
以上所有示例都显示在图中，其中导数以红色绘制。请注意，圆的导数也定义了空间中的一个圆。
参数函数及其导数
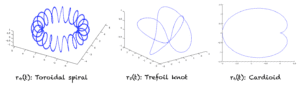
更复杂的示例
一旦您掌握了这些函数的基本知识，您就可以通过定义空间中的各种形状和曲线来获得很多乐趣。数学界使用的一些其他流行示例如下所示，并在图中进行了说明。
圆环螺旋
r_4(t) = (4 + sin(20t))cos(t)i + (4 + sin(20t))sin(t)j + cos(20t)k
三叶草结:
r_5(t) = (2 + cos(1.5t)cos (t)i + (2 + cos(1.5t))sin(t)j + sin(1.5t)k
心形线
r_6(t) = cos(t)(1-cos(t))i + sin(t)(1-cos(t))j
更复杂的曲线
向量值函数在机器学习中的重要性
向量值函数在机器学习算法中起着重要作用。作为标量值函数的扩展，您会在多类分类和多标签问题等任务中遇到它们。核方法是机器学习的一个重要领域，可能涉及计算向量值函数，这些函数随后可用于多任务学习或迁移学习。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 积分向量函数
- 抛射体运动
- 空间弧长
- 向量输出的核方法
如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
教程
资源
- 关于机器学习微积分书籍的额外资源
书籍
- 《托马斯微积分》，第14版，2017年。（基于 George B. Thomas 的原创作品，由 Joel Hass, Christopher Heil, Maurice Weir修订）
- 微积分，第 3 版，2017 年。（Gilbert Strang）
- 《微积分》，第8版，2015年。（James Stewart）
总结
在本教程中，您了解了向量函数是什么以及如何对它们进行微分。
具体来说，你学到了：
- 向量函数的定义
- 参数曲线
- 向量函数的微分
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
暂无评论。