拉普拉斯算子最初由皮埃尔-西蒙·拉普拉斯(Pierre-Simon de Laplace)应用于天体力学或外层空间物体运动的研究,因此以他的名字命名。
自那时以来,拉普拉斯算子一直被用来描述许多不同的现象,从电势、热和流体流动的扩散方程,到量子力学。它也被重塑为离散空间,并在图像处理和谱聚类等应用中使用。
在本教程中,您将了解到拉普拉斯算子的温和介绍。
完成本教程后,您将了解:
- 拉普拉斯算子的定义及其与散度的关系。
- 拉普拉斯算子与 Hessian 的关系。
- 连续拉普拉斯算子如何被重塑为离散空间,并应用于图像处理和谱聚类。
让我们开始吧。

拉普拉斯算子的温和介绍
照片由 Aziz Acharki 拍摄,部分权利保留。
教程概述
本教程分为两部分;它们是
- 拉普拉斯算子
- 散度概念
- 连续拉普拉斯算子
- 离散拉普拉斯算子
先决条件
对于本教程,我们假设您已经了解以下内容:
您可以通过点击上面给出的链接来复习这些概念。
拉普拉斯算子
拉普拉斯算子(或通常称为拉普拉斯算子)是函数梯度的散度。
为了更好地理解前面的陈述,最好从理解“散度”的概念开始。
散度概念
散度是一个作用于矢量场的向量算子。后者可以被认为是表示液体或气体的流动,其中矢量场中的每个向量代表移动流体的速度向量。
粗略地说,散度衡量流体在某一点的聚集或扩散的趋势……
– 第 432 页,单变量和多变量微积分,2020 年。
使用 nabla(或 del)算子 ∇,散度表示为 ∇ .,当作用于矢量场时产生一个标量值,衡量每个点的“流体”量。在笛卡尔坐标系中,矢量场 F = ⟨f, g, h⟩ 的散度由下式给出
虽然散度计算涉及散度算子的应用(而非乘法运算),但其符号中的点令人联想到点积,点积涉及两个等长序列(在此例中为 ∇ 和 F)的分量相乘,并对结果项求和。
连续拉普拉斯算子
让我们回到拉普拉斯算子的定义。
我们回顾一下,二维函数 f 的梯度给出为
那么,f 的拉普拉斯算子(即梯度的散度)可以定义为所有非混合的二阶偏导数之和
等价地,它也可以看作是函数 Hessian H(f) 的迹 (tr)。迹定义了方阵 n×n 的主对角线元素之和,在本例中即 Hessian,也是其特征值之和。请记住,Hessian 矩阵在对角线上包含非混合的二阶偏导数。
迹的一个重要性质是它在“基变换”下不变。我们已经在笛卡尔坐标系中定义了拉普拉斯算子。在极坐标系中,我们可以这样定义它:
迹在基变换下的不变性意味着拉普拉斯算子可以在不同的坐标空间中定义,但它在笛卡尔坐标空间中的某个点 (x, y) 和极坐标空间中的同一点 (r, θ) 处会得到相同的值。
回想一下,我们还提到二阶导数可以提供关于函数曲率的信息。因此,直观上,我们可以认为拉普拉斯算子也通过这些二阶导数的求和,提供了关于函数局部曲率的信息。
连续拉普拉斯算子已被用于描述许多物理现象,例如电势和热流的扩散方程。
想开始学习机器学习微积分吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
离散拉普拉斯算子
与连续拉普拉斯算子类似的是离散算子,它被公式化以便应用于离散网格,例如图像中的像素值或图。
让我们看看拉普拉斯算子如何为这两种应用重塑。
在图像处理中,拉普拉斯算子以数字滤波器的形式实现,当应用于图像时,可用于边缘检测。在某种意义上,我们可以认为图像处理中使用的拉普拉斯算子也为我们提供了关于函数在某个特定点 (x, y) 处如何弯曲(或“弯折”)的信息。
在这种情况下,离散拉普拉斯算子(或滤波器)是通过将两个一维二阶导数滤波器组合成一个二维滤波器来构建的。
在机器学习中,离散拉普拉斯算子从图中提取的信息可用于数据聚类。
考虑一个图 G = (V, E),它具有有限数量的 V 个顶点和 E 条边。其拉普拉斯矩阵 L 可以根据度矩阵 D(包含每个顶点的连接信息)和邻接矩阵 A(表示图中相邻的顶点对)来定义。
L = D – A
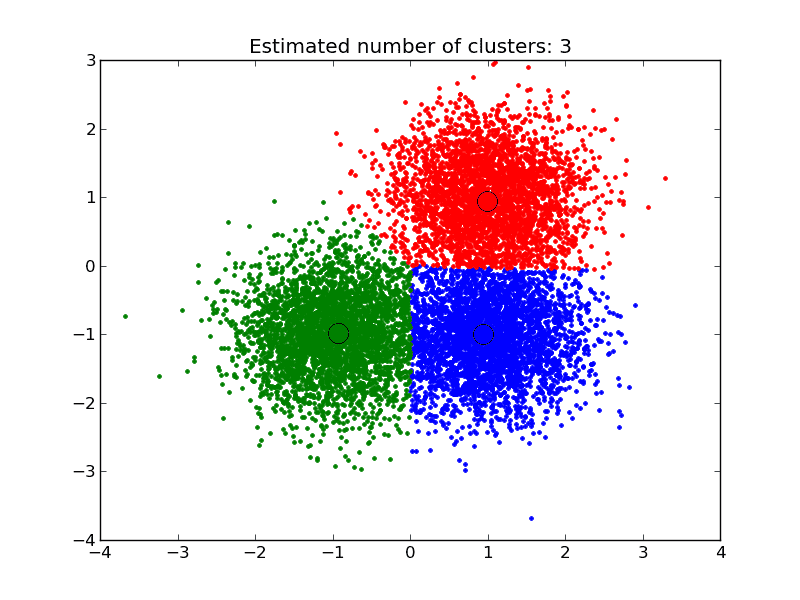
谱聚类可以通过应用一些标准的聚类方法(如 k-means)到拉普拉斯矩阵的特征向量上来实现,从而将图节点(或数据点)划分为子集。
这样做可能出现的一个问题是,对于大型数据集,拉普拉斯矩阵的特征分解(或特征向量提取)可能难以承受。深度学习的使用已被提出来解决这个问题,其中训练一个深度神经网络,使其输出近似于图拉普拉斯算子的特征向量。在这种情况下,神经网络通过约束优化方法进行训练,以强制执行网络输出的正交性。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 单变量和多变量微积分, 2020.
- 图像和视频处理手册,2005 年。
文章
论文
- SpectralNet:使用深度神经网络的谱聚类, 2018.
总结
在本教程中,您了解了拉普拉斯算子的温和介绍。
具体来说,你学到了:
- 拉普拉斯算子的定义及其与散度的关系。
- 拉普拉斯算子与 Hessian 的关系。
- 连续拉普拉斯算子如何被重塑为离散空间,并应用于图像处理和谱聚类。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。

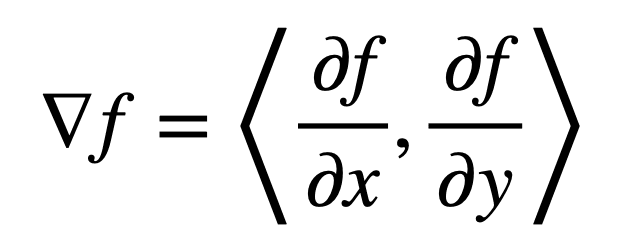
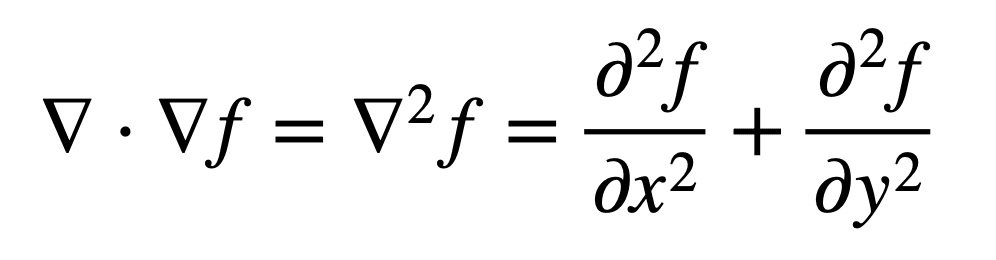
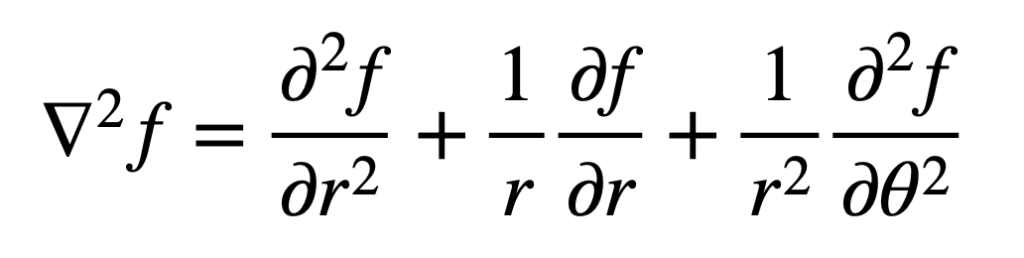






很棒的数学解释!
谢谢!
在结尾或总结时,我认为我们是在讨论数学导数(算子)……
也就是说,事物相对于其他事物的变化(分数)……而这种变化分析提供了关于其他物理特征或模式(在图像分析中)的丰富信息。
感谢您的评论!
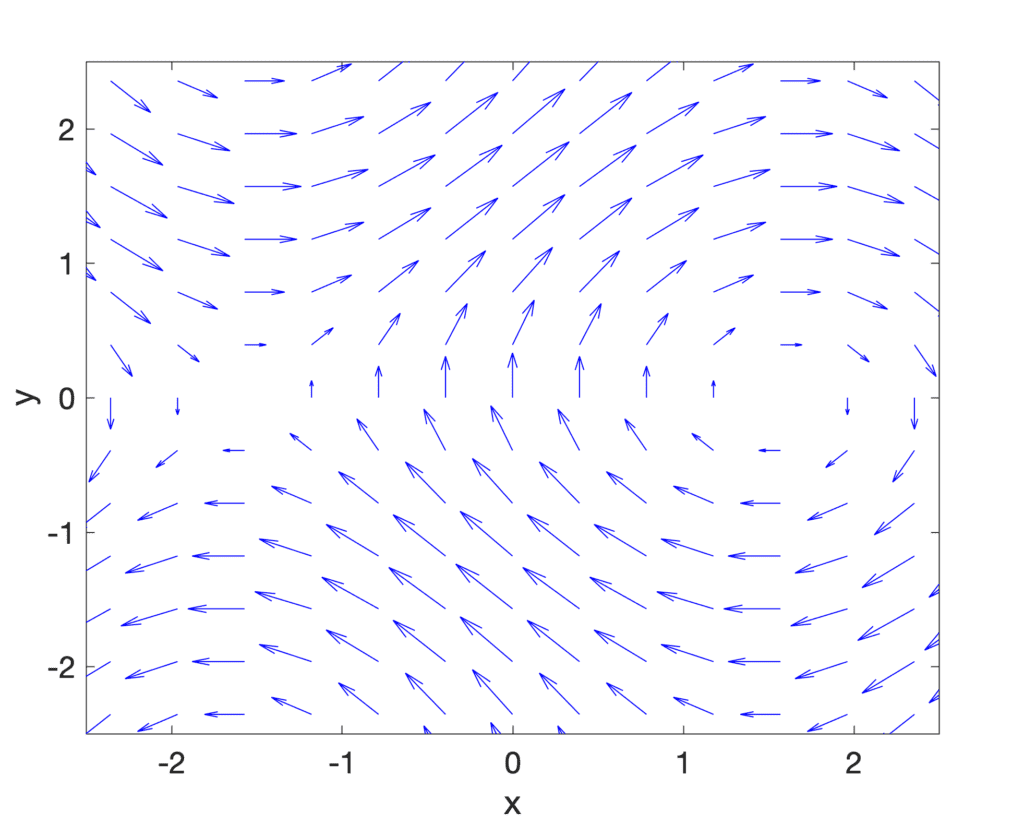
矢量场不可能是 (cos x, sin y)。在 (0,0) 处有一个垂直箭头。你可能翻转了坐标。
感谢您的反馈 Alfredo!
图是 (sin(y), cos(x))
我正在读新不伦瑞克大学化学工程专业的二年级。我正在寻找关于热传输方程中拉普拉斯算子的快速有意义的复习,我在这里找到了一些见解,还不错!
感谢您的反馈 Zulfiqar!虽然我们的内容不是学术性的,但我们希望它能成为一个很好的起点。
粗略地说,散度衡量流体在某一点的聚集或扩散的趋势……
– 第 432 页,“单变量和多变量微积分”,2020 年。
这其实是在第 433 页,第 16.5 章“散度和旋度”。
感谢 KP!我们很感激!