支持向量机 (SVM) 分类器背后的数学原理非常精妙。不仅要学习 SVM 的基本模型,还要了解如何从零开始实现整个模型,这一点很重要。这是我们关于 SVM 系列教程的延续。在本系列的第一部分和第二部分中,我们讨论了线性 SVM 背后的数学模型。在本教程中,我们将展示如何使用 Python SciPy 库中提供的优化例程构建 SVM 线性分类器。
完成本教程后,您将了解:
- 如何使用 SciPy 的优化例程
- 如何定义目标函数
- 如何定义界限和线性约束
- 如何在 Python 中实现您自己的 SVM 分类器
让我们开始吧。
教程概述
本教程分为两部分;它们是:
- SVM 的优化问题
- Python 中优化问题的解决方案
- 定义目标函数
- 定义界限和线性约束
- 使用不同的 C 值解决问题
先决条件
本教程假设您已熟悉以下主题。您可以点击各个链接以获取更多详细信息。
符号和假设
基本的 SVM 机器假定为二分类问题。假设我们有 $m$ 个训练点,每个点都是一个 $n$ 维向量。我们将使用以下符号:
- $m$:总训练点数
- $n$:每个训练点的维度
- $x$:数据点,是一个 $n$ 维向量
- $i$: 用于索引训练点的下标。$0 \leq i < m$
- $k$:用于索引训练点的下标。$0 \leq k < m$
- $j$:用于索引训练点每个维度的下标
- $t$:数据点的标签。它是一个 $m$ 维向量,其中 $t_i \in \{-1, +1\}$
- $T$:转置运算符
- $w$:权重向量,表示超平面的系数。它也是一个 $n$ 维向量
- $\alpha$:拉格朗日乘数向量,也是一个 $m$ 维向量
- $C$:用户定义的惩罚因子/正则化常数
SVM 优化问题
SVM 分类器最大化以下拉格朗日对偶函数:
$$
L_d = -\frac{1}{2} \sum_i \sum_k \alpha_i \alpha_k t_i t_k (x_i)^T (x_k) + \sum_i \alpha_i
$$
上述函数受以下约束:
\begin{eqnarray}
0 \leq \alpha_i \leq C, & \forall i\\
\sum_i \alpha_i t_i = 0& \\
\end{eqnarray}
我们所要做的就是找到与每个训练点相关的拉格朗日乘数 $\alpha$,同时满足上述约束。
想开始学习机器学习微积分吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
SVM 的 Python 实现
我们将使用 SciPy optimize 包来寻找拉格朗日乘数的最佳值,并计算软间隔和分离超平面。
导入部分和常量
让我们编写用于优化、绘图和合成数据生成的导入部分。
|
1 2 3 4 5 6 7 8 9 |
import numpy as np # 用于优化 from scipy.optimize import Bounds, BFGS from scipy.optimize import LinearConstraint, minimize # 用于绘图 import matplotlib.pyplot as plt import seaborn as sns # 用于生成数据集 import sklearn.datasets as dt |
我们还需要以下常量来检测所有在数值上接近零的 alpha,因此我们需要定义自己的零阈值。
|
1 |
ZERO = 1e-7 |
定义数据点和标签
让我们定义一个非常简单的数据集、相应的标签和用于绘制这些数据的简单例程。另外,如果向绘图函数提供了一串 alpha 值,它还将用相应的 alpha 值标记所有支持向量。回想一下,支持向量是那些 $\alpha>0$ 的点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
dat = np.array([[0, 3], [-1, 0], [1, 2], [2, 1], [3,3], [0, 0], [-1, -1], [-3, 1], [3, 1]]) labels = np.array([1, 1, 1, 1, 1, -1, -1, -1, -1]) def plot_x(x, t, alpha=[], C=0): sns.scatterplot(dat[:,0], dat[:, 1], style=labels, hue=labels, markers=['s', 'P'], palette=['magenta', 'green']) if len(alpha) > 0: alpha_str = np.char.mod('%.1f', np.round(alpha, 1)) ind_sv = np.where(alpha > ZERO)[0] for i in ind_sv: plt.gca().text(dat[i,0], dat[i, 1]-.25, alpha_str[i] ) plot_x(dat, labels) |
minimize() 函数
我们来看看 scipy.optimize 库中的 minimize() 函数。它需要以下参数:
- 需要最小化的目标函数。在我们的例子中是拉格朗日对偶函数。
- 优化所针对变量的初始值。在这个问题中,我们需要确定拉格朗日乘数 $\alpha$。我们将所有 $\alpha$ 随机初始化。
- 用于优化的方法。我们将使用
trust-constr。 - 对 $\alpha$ 的线性约束。
- 对 $\alpha$ 的界限。
定义目标函数
我们的目标函数是上面定义的 $L_d$,它必须最大化。由于我们使用 minimize() 函数,我们必须将 $L_d$ 乘以 (-1) 才能最大化它。其实现如下。目标函数的第一个参数是进行优化的变量。我们还需要训练点和相应的标签作为附加参数。
您可以使用矩阵来缩短下面给出的 lagrange_dual() 函数的代码。但是,在本教程中,为了清晰起见,它被保持得非常简单。
|
1 2 3 4 5 6 7 8 9 |
# 目标函数 def lagrange_dual(alpha, x, t): result = 0 ind_sv = np.where(alpha > ZERO)[0] for i in ind_sv: for k in ind_sv: result = result + alpha[i]*alpha[k]*t[i]*t[k]*np.dot(x[i, :], x[k, :]) result = 0.5*result - sum(alpha) return result |
定义线性约束
每个点上 alpha 的线性约束由下式给出:
$$
\sum_i \alpha_i t_i = 0
$$
我们也可以将其写成:
$$
\alpha_0 t_0 + \alpha_1 t_1 + \ldots \alpha_m t_m = 0
$$
LinearConstraint() 方法要求所有约束都写成矩阵形式,即:
\begin{equation}
0 =
\begin{bmatrix}
t_0 & t_1 & \ldots t_m
\end{bmatrix}
\begin{bmatrix}
\alpha_0\\ \alpha_1 \\ \vdots \\ \alpha_m
\end{bmatrix}
= 0
\end{equation}
第一个矩阵是 LinearConstraint() 方法中的第一个参数。左右边界是第二个和第三个参数。
|
1 2 |
linear_constraint = LinearConstraint(labels, [0], [0]) print(linear_constraint) |
|
1 |
<scipy.optimize._constraints.LinearConstraint object at 0x12c87f5b0> |
定义界限
alpha 的界限使用 Bounds() 方法定义。所有 alpha 都被限制在 0 和 $C$ 之间。以下是 $C=10$ 的示例。
|
1 2 |
bounds_alpha = Bounds(np.zeros(dat.shape[0]), np.full(dat.shape[0], 10)) print(bounds_alpha) |
|
1 |
Bounds(array([0., 0., 0., 0., 0., 0., 0., 0., 0.]), array([10, 10, 10, 10, 10, 10, 10, 10, 10])) |
定义寻找 Alpha 的函数
让我们编写一个通用例程,在给定参数 x、t 和 C 的情况下,找到 alpha 的最优值。目标函数需要额外的参数 x 和 t,这些参数通过 minimize() 中的 args 传递。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
def optimize_alpha(x, t, C): m, n = x.shape np.random.seed(1) # 将 alphas 初始化为随机值 alpha_0 = np.random.rand(m)*C # 定义约束 linear_constraint = LinearConstraint(t, [0], [0]) # 定义界限 bounds_alpha = Bounds(np.zeros(m), np.full(m, C)) # 找到 alpha 的最优值 result = minimize(lagrange_dual, alpha_0, args = (x, t), method='trust-constr', hess=BFGS(), constraints=[linear_constraint], bounds=bounds_alpha) # alpha 的最优值在 result.x 中 alpha = result.x return alpha |
确定超平面
超平面的表达式由下式给出:
$$
w^T x + w_0 = 0
$$
对于超平面,我们需要权重向量 $w$ 和常数 $w_0$。权重向量由下式给出:
$$
w = \sum_i \alpha_i t_i x_i
$$
如果训练点太多,最好只使用 $\alpha>0$ 的支持向量来计算权重向量。
对于 $w_0$,我们将从每个支持向量 $s$(其中 $\alpha_s < C$)计算它,然后取平均值。对于单个支持向量 $x_s$, $w_0$ 由下式给出:
$$
w_0 = t_s – w^T x_s
$$
支持向量的 alpha 在数值上不能正好等于 C。因此,我们可以从 C 中减去一个小的常量,以找到所有 $\alpha_s < C$ 的支持向量。这在 get_w0() 函数中完成。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def get_w(alpha, t, x): m = len(x) # 获取所有支持向量 w = np.zeros(x.shape[1]) for i in range(m): w = w + alpha[i]*t[i]*x[i, :] return w def get_w0(alpha, t, x, w, C): C_numeric = C-ZERO # alpha ind_sv = np.where((alpha > ZERO)&(alpha < C_numeric))[0] w0 = 0.0 for s in ind_sv: w0 = w0 + t[s] - np.dot(x[s, :], w) # 取平均值 w0 = w0 / len(ind_sv) return w0 |
分类测试点
要分类测试点 $x_{test}$,我们使用 $y(x_{test})$ 的符号:
$$
\text{label}_{x_{test}} = \text{sign}(y(x_{test})) = \text{sign}(w^T x_{test} + w_0)
$$
让我们编写相应的函数,它可以接受测试点数组以及 $w$ 和 $w_0$ 作为参数,并对各种点进行分类。我们还添加了第二个函数用于计算错误分类率。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def classify_points(x_test, w, w0): # 获取 y(x_test) predicted_labels = np.sum(x_test*w, axis=1) + w0 predicted_labels = np.sign(predicted_labels) # 如果为零,则任意分配标签 +1 predicted_labels[predicted_labels==0] = 1 return predicted_labels def misclassification_rate(labels, predictions): total = len(labels) errors = sum(labels != predictions) return errors/total*100 |
绘制间隔和超平面
我们还定义函数来绘制超平面和软间隔。
|
1 2 3 4 5 6 7 8 9 10 11 |
def plot_hyperplane(w, w0): x_coord = np.array(plt.gca().get_xlim()) y_coord = -w0/w[1] - w[0]/w[1] * x_coord plt.plot(x_coord, y_coord, color='red') def plot_margin(w, w0): x_coord = np.array(plt.gca().get_xlim()) ypos_coord = 1/w[1] - w0/w[1] - w[0]/w[1] * x_coord plt.plot(x_coord, ypos_coord, '--', color='green') yneg_coord = -1/w[1] - w0/w[1] - w[0]/w[1] * x_coord plt.plot(x_coord, yneg_coord, '--', color='magenta') |
启动 SVM
现在是运行 SVM 的时候了。函数 display_SVM_result() 将帮助我们可视化一切。我们将 alpha 初始化为随机值,定义 C 并在此函数中找到 alpha 的最佳值。我们还将绘制超平面、间隔和数据点。支持向量也将标上其相应的 alpha 值。图的标题将是错误百分比和支持向量的数量。
|
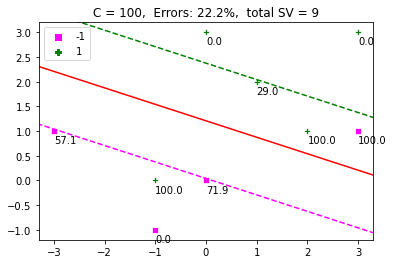
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def display_SVM_result(x, t, C): # 获取 alpha 值 alpha = optimize_alpha(x, t, C) # 获取权重 w = get_w(alpha, t, x) w0 = get_w0(alpha, t, x, w, C) plot_x(x, t, alpha, C) xlim = plt.gca().get_xlim() ylim = plt.gca().get_ylim() plot_hyperplane(w, w0) plot_margin(w, w0) plt.xlim(xlim) plt.ylim(ylim) # 获取错误分类率并将其显示为标题 predictions = classify_points(x, w, w0) err = misclassification_rate(t, predictions) title = 'C = ' + str(C) + ', Errors: ' + '{:.1f}'.format(err) + '%' title = title + ', total SV = ' + str(len(alpha[alpha > ZERO])) plt.title(title) display_SVM_result(dat, labels, 100) plt.show() |
C 的影响
如果您将 C 的值更改为 $\infty$,那么软间隔将变为硬间隔,对错误没有任何容忍度。我们上面定义的问题在这种情况下是无法解决的。让我们生成一组人工点,看看 C 对分类的影响。为了理解整个问题,我们将使用一个简单的数据集,其中正例和负例是可分离的。
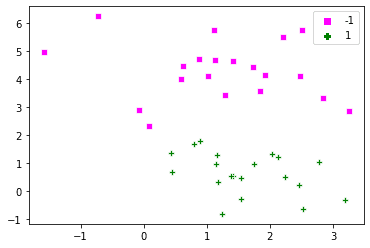
以下是通过 make_blobs() 生成的点:
|
1 2 3 4 5 |
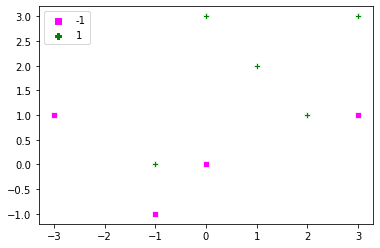
dat, labels = dt.make_blobs(n_samples=[20,20], cluster_std=1, random_state=0) labels[labels==0] = -1 plot_x(dat, labels) |
现在让我们定义不同的 C 值并运行代码。
|
1 2 3 4 5 6 7 8 9 |
fig = plt.figure(figsize=(8,25)) i=0 C_array = [1e-2, 100, 1e5] for C in C_array: fig.add_subplot(311+i) display_SVM_result(dat, labels, C) i = i + 1 |
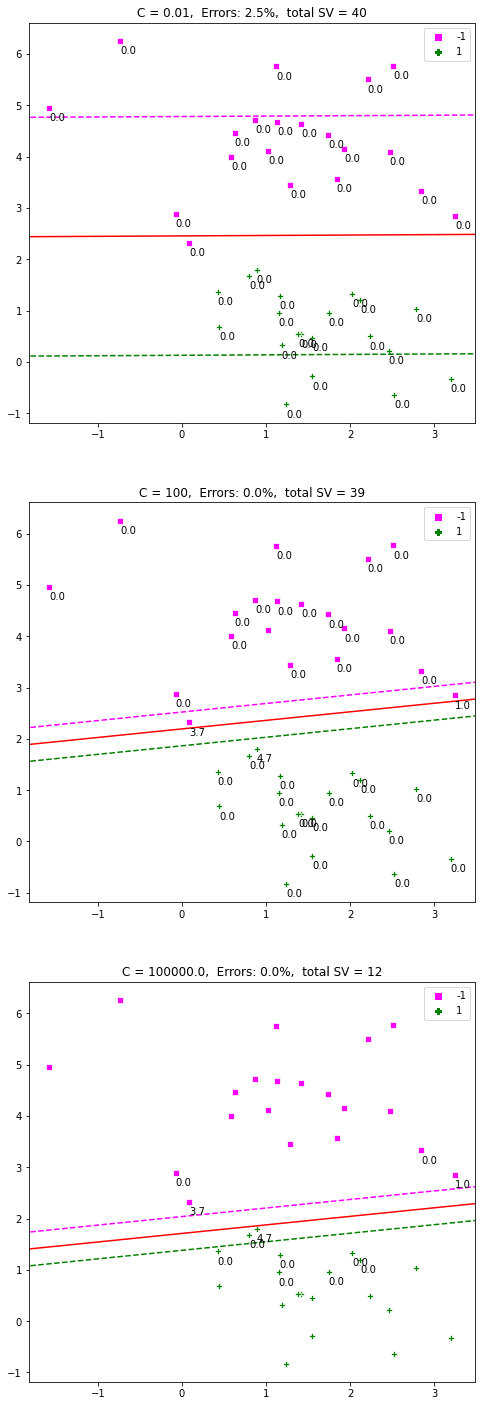 结果评论
结果评论
上图是一个很好的例子,它表明增加 $C$ 会减小间隔。较高的 $C$ 值会对错误施加更严格的惩罚。较小的值允许更宽的间隔和更多的错误分类。因此,$C$ 定义了间隔最大化和分类错误之间的权衡。
合并代码
以下是合并后的代码,您可以将其粘贴到您的 Python 文件中并在您端运行。您可以尝试不同的 $C$ 值,并尝试作为 minimize() 函数参数的不同优化方法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
import numpy as np # 用于优化 from scipy.optimize import Bounds, BFGS from scipy.optimize import LinearConstraint, minimize # 用于绘图 import matplotlib.pyplot as plt import seaborn as sns # 用于生成数据集 import sklearn.datasets as dt ZERO = 1e-7 def plot_x(x, t, alpha=[], C=0): sns.scatterplot(dat[:,0], dat[:, 1], style=labels, hue=labels, markers=['s', 'P'], palette=['magenta', 'green']) if len(alpha) > 0: alpha_str = np.char.mod('%.1f', np.round(alpha, 1)) ind_sv = np.where(alpha > ZERO)[0] for i in ind_sv: plt.gca().text(dat[i,0], dat[i, 1]-.25, alpha_str[i] ) # 目标函数 def lagrange_dual(alpha, x, t): result = 0 ind_sv = np.where(alpha > ZERO)[0] for i in ind_sv: for k in ind_sv: result = result + alpha[i]*alpha[k]*t[i]*t[k]*np.dot(x[i, :], x[k, :]) result = 0.5*result - sum(alpha) return result def optimize_alpha(x, t, C): m, n = x.shape np.random.seed(1) # 将 alphas 初始化为随机值 alpha_0 = np.random.rand(m)*C # 定义约束 linear_constraint = LinearConstraint(t, [0], [0]) # 定义界限 bounds_alpha = Bounds(np.zeros(m), np.full(m, C)) # 找到 alpha 的最优值 result = minimize(lagrange_dual, alpha_0, args = (x, t), method='trust-constr', hess=BFGS(), constraints=[linear_constraint], bounds=bounds_alpha) # alpha 的最优值在 result.x 中 alpha = result.x return alpha def get_w(alpha, t, x): m = len(x) # 获取所有支持向量 w = np.zeros(x.shape[1]) for i in range(m): w = w + alpha[i]*t[i]*x[i, :] return w def get_w0(alpha, t, x, w, C): C_numeric = C-ZERO # alpha ind_sv = np.where((alpha > ZERO)&(alpha < C_numeric))[0] w0 = 0.0 for s in ind_sv: w0 = w0 + t[s] - np.dot(x[s, :], w) # 取平均值 w0 = w0 / len(ind_sv) return w0 def classify_points(x_test, w, w0): # 获取 y(x_test) predicted_labels = np.sum(x_test*w, axis=1) + w0 predicted_labels = np.sign(predicted_labels) # 如果为零,则任意分配标签 +1 predicted_labels[predicted_labels==0] = 1 return predicted_labels def misclassification_rate(labels, predictions): total = len(labels) errors = sum(labels != predictions) return errors/total*100 def plot_hyperplane(w, w0): x_coord = np.array(plt.gca().get_xlim()) y_coord = -w0/w[1] - w[0]/w[1] * x_coord plt.plot(x_coord, y_coord, color='red') def plot_margin(w, w0): x_coord = np.array(plt.gca().get_xlim()) ypos_coord = 1/w[1] - w0/w[1] - w[0]/w[1] * x_coord plt.plot(x_coord, ypos_coord, '--', color='green') yneg_coord = -1/w[1] - w0/w[1] - w[0]/w[1] * x_coord plt.plot(x_coord, yneg_coord, '--', color='magenta') def display_SVM_result(x, t, C): # 获取 alpha 值 alpha = optimize_alpha(x, t, C) # 获取权重 w = get_w(alpha, t, x) w0 = get_w0(alpha, t, x, w, C) plot_x(x, t, alpha, C) xlim = plt.gca().get_xlim() ylim = plt.gca().get_ylim() plot_hyperplane(w, w0) plot_margin(w, w0) plt.xlim(xlim) plt.ylim(ylim) # 获取错误分类率并将其显示为标题 predictions = classify_points(x, w, w0) err = misclassification_rate(t, predictions) title = 'C = ' + str(C) + ', Errors: ' + '{:.1f}'.format(err) + '%' title = title + ', total SV = ' + str(len(alpha[alpha > ZERO])) plt.title(title) dat = np.array([[0, 3], [-1, 0], [1, 2], [2, 1], [3,3], [0, 0], [-1, -1], [-3, 1], [3, 1]]) labels = np.array([1, 1, 1, 1, 1, -1, -1, -1, -1]) plot_x(dat, labels) plt.show() display_SVM_result(dat, labels, 100) plt.show() dat, labels = dt.make_blobs(n_samples=[20,20], cluster_std=1, random_state=0) labels[labels==0] = -1 plot_x(dat, labels) fig = plt.figure(figsize=(8,25)) i=0 C_array = [1e-2, 100, 1e5] for C in C_array: fig.add_subplot(311+i) display_SVM_result(dat, labels, C) i = i + 1 |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
文章
API 参考
总结
在本教程中,您学习了如何从零开始实现 SVM 分类器。
具体来说,你学到了:
- 如何编写 SVM 优化问题的目标函数和约束
- 如何编写代码从拉格朗日乘数中确定超平面
- C 对确定间隔的影响
您对本文中讨论的 SVM 有任何疑问吗?请在下面的评论中提出您的问题,我将尽力回答。








不工作
嗨 Petar……具体是哪个部分不工作?
此致,
嗯,我复制了完整的合并代码,但收到了这个错误消息:
plot_x
sns.scatterplot(dat[:,0], dat[:, 1], style=labels,
TypeError: scatterplot() 接受 0 到 1 个位置参数,但给出了 2 个位置参数(和 4 个仅限关键字参数)。
嗨 Mac_S04……以下讨论可能会对此场景提供一些清晰度
https://stackoverflow.com/questions/75800646/typeerror-jointplot-takes-from-0-to-1-positional-arguments-but-2-positional-a