机器学习和数据科学算法中最常用的函数之一是多项式或涉及 x 幂次的函数。因此，理解如何计算此类函数的导数非常重要。
在本教程中，您将学习如何计算 x 的幂函数和多项式的导数。
完成本教程后，您将了解：
- 计算多项式导数的一般规则
- 求涉及 x 的任何非零实数幂次的函数导数的一般规则
让我们开始吧。
幂函数和多项式的导数，图片由 Misbah Ghufran 提供，保留部分权利
教程概述
本教程分为两部分；它们是
- 涉及 x 整数幂次的函数的导数
- 具有 x 的任何非零实数幂次的函数的微分
两个函数和的导数
让我们从寻找一个管理两个函数之和的简单规则开始。假设我们有两个函数 f(x) 和 g(x)，那么它们的和的导数可以如下求出。如果需要复习，您可以参考导数的定义。
两个函数和的导数
这里我们有一个通用规则，即两个函数之和的导数是各个函数导数之和。
x 的整数幂次的导数
在讨论 x 的整数幂次的导数之前，我们先回顾一下二项式定理，它告诉我们如何展开以下表达式（其中 C(n,k) 是组合函数）
(a+b)^n = a^n + C(n,1)a^(n-1)b + C(n,2)a^(n-2)b^2 + … + C(n,n-1)ab^(n-1) + b^n
我们将推导一个简单的规则，用于求涉及 x^n 的函数的导数，其中 n 是一个整数且 n>0。让我们回到本教程中讨论的导数定义，并将其应用于 kx^n，其中 k 是一个常数。
kx^n 的导数
以下是应用此规则的一些示例
- x^2 的导数是 2x
- 3x^5 的导数是 15x^4
- 4x^9 的导数是 36x^8
如何微分多项式？
这两个规则，即两个函数之和的导数规则和 x 整数幂次的导数规则，使我们能够微分多项式。如果我们有一个 n 次多项式，我们可以将其视为涉及 x 的不同幂次的单个函数之和。假设我们有一个 n 次多项式 P(x)，那么它的导数 P'(x) 由下式给出：
多项式的导数
这表明 n 次多项式的导数实际上是一个 (n-1) 次多项式。
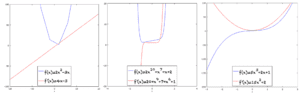
示例
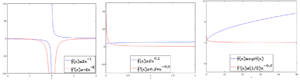
下面显示了一些示例，其中多项式函数及其导数都绘制在一起。蓝色曲线表示函数本身，而红色曲线表示该函数的导数。
多项式函数及其导数的示例
x 的非整数幂次呢？
上述推导的规则也适用于 x 的非整数实数幂次，这些幂次可以是分数、负数或无理数。一般规则如下，其中 a 和 k 可以是任何不等于零的实数。
f(x) = kx^a
f'(x) = kax^(a-1)
一些例子是
- x^(0.2) 的导数是 (0.2)x^(-0.8)
- x^(????) 的导数是 ????x^(????-1)
- x^(-3/4) 的导数是 (-3/4)x^(-7/4)
这里有一些例子，它们与它们的导数一起绘制。同样，蓝色曲线表示函数本身，红色曲线表示相应的导数
涉及 x 实数幂次的表达式导数示例
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 两个函数乘积的导数规则
- 有理函数的导数规则
- 积分
如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。
延伸阅读¶
如果您想深入了解，本节提供了更多关于该主题的资源。
教程
资源¶
- 关于机器学习微积分书籍的额外资源
书籍
- 《托马斯微积分》，第14版，2017年。（基于 George B. Thomas 的原创作品，由 Joel Hass, Christopher Heil, Maurice Weir修订）
- 微积分，第 3 版，2017 年。（Gilbert Strang）
- 《微积分》，第8版，2015年。（James Stewart）
总结
在本教程中，您学习了如何微分多项式函数和涉及 x 的非整数幂次和的函数。
具体来说，你学到了：
- 两个函数之和的导数
- 常数乘以 x 的整数幂次的导数
- 多项式函数的导数
- 涉及 x 的非整数幂次表达式之和的导数
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
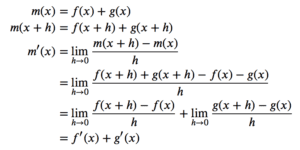
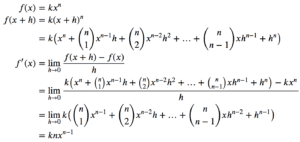
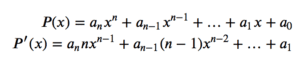
暂无评论。