在评估函数极限时,我们经常会遇到不定形式,而极限在数学和微积分中起着重要的作用。它们对于学习导数、梯度、Hessian 等概念至关重要。
在本教程中,您将学习如何评估不定形式的极限以及用于求解它们的洛必达法则。
完成本教程后,您将了解:
- 如何评估具有 0/0 和 ∞/∞ 形式的不定类型的函数极限
- 用于评估不定类型的洛必达法则
- 如何转换更复杂的不定类型并将其应用于洛必达法则
让我们开始吧。
教程概述
本教程分为两部分;它们是:
- 0/0 和 ∞/∞ 形式的不定形式
- 如何将洛必达法则应用于这些类型
- 这两个不定类型的求解示例
- 更复杂的不定类型
- 如何将更复杂的不定类型转换为 0/0 和 ∞/∞ 形式
- 此类类型的求解示例
先决条件
本教程需要对以下两个主题有基本了解
如果您不熟悉这些主题,可以点击上面的链接进行回顾。
什么是“不定形式”?
在评估极限时,我们会遇到一些情况,其中基本极限评估规则可能会失效。例如,对于有理函数,我们可以应用商法则:
lim(x→a) f(x)/g(x) = (lim(x→a)f(x))/(lim(x→a)g(x)) 如果 lim(x→a)g(x)≠0
上述规则只有在当 x 趋近于 a 时分母中的表达式不趋近于零时才能应用。当分子和分母都趋近于零时,情况会更复杂。这被称为 0/0 型的不定形式。同样,也有 ∞/∞ 型的不定形式,表示为:
lim(x→a) f(x)/g(x) = (lim(x→a)f(x))/(lim(x→a)g(x)) 当 lim(x→a)f(x)=∞ 且 lim(x→a)g(x)= ∞ 时
什么是洛必达法则?
洛必达法则陈述如下:
何时应用洛必达法则
需要注意的一个重要点是,洛必达法则仅在满足 f(x) 和 g(x) 的条件时适用。例如:
- lim(????→0) sin(x)/(x+1) 不能应用洛必达法则,因为它不是 0/0 形式
- lim(????→0) sin(x)/x 可以应用该法则,因为它属于 0/0 形式
- lim(????→∞) (e^x)/(1/x+1) 不能应用洛必达法则,因为它不是 ∞/∞ 形式
- lim(????→∞) (e^x)/x 可以应用洛必达法则,因为它属于 ∞/∞ 形式
0/0 和 ∞/∞ 的示例
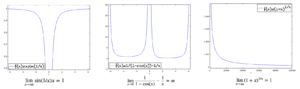
下面展示了这两种类型的几个示例以及如何求解它们。您也可以参考下图来查看这些函数。
示例 1.1:0/0
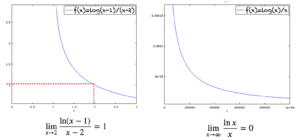
求极限 lim(????→2) ln(x-1)/(x-2) (参见图中的左图)
示例 1.2:∞/∞
求极限 lim(????→∞) ln(x)/x (参见图中的右图)
更多不定形式
洛必达法则只告诉我们如何处理 0/0 或 ∞/∞ 形式。然而,还有更多涉及乘积、差和幂的不定形式。那么我们如何处理其余的呢?我们可以利用一些巧妙的数学技巧将乘积、差和幂转换为商。这使得我们能够轻松地将洛必达法则应用于几乎所有不定形式。下表显示了各种不定形式以及如何处理它们。
示例
以下示例展示了如何将一种不定形式转换为 0/0 或 ∞/∞ 形式并应用洛必达法则来求解极限。在演算示例后,您还可以查看所有计算了极限的函数的图。
示例 2.1:0·∞
求极限 lim(????→∞) x·sin(1/x) (参见图中的第一个图)
示例 2.2:∞-∞
求极限 lim(????→0) 1/(1-cos(x)) – 1/x (参见下图中的第二个图)
示例 2.3:幂形式
求极限 lim(????→∞) (1+x)^(1/x) (参见下图中的第三个图)
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 柯西中值定理
- 罗尔定理
如果您探索了这些扩展内容中的任何一个,我很想知道。请在下面的评论中发布您的发现。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
资源
- 机器学习微积分书籍 的其他资源
书籍
- 《托马斯微积分》,第14版,2017年。(基于 George B. Thomas 的原创作品,由 Joel Hass, Christopher Heil, Maurice Weir修订)
- 微积分,第三版,2017年。(Gilbert Strang)
- 《微积分》,第8版,2015年。(James Stewart)
总结
在本教程中,您学习了不定形式的概念以及如何求解它们。
具体来说,你学到了:
- 0/0 和 ∞/∞ 类型的不定形式
- 求解 0/0 和 ∞/∞ 类型的洛必达法则
- 0·∞、∞-∞ 和幂形式的不定形式,以及如何求解它们。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。


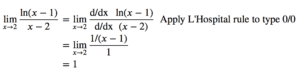


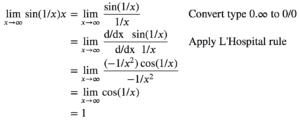
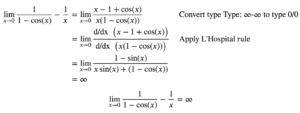







感谢分享,但我有一个问题:在示例 2.3 中,指数函数的极限为什么在第三个等式中等于极限的指数?
您好 Yasser
这是评估极限的规则之一。请参阅这篇文章。这篇文章中有一个包含规则的表格
https://machinelearning.org.cn/a-gentle-introduction-to-evaluating-limits/
希望这有帮助。
因为指数(e)只是一个介于 2 和 3 之间的常数。由于 'e' 的幂是一个变量,在应用极限时会产生不定形式。因此,极限仅应用于幂或变量,或者只是指数函数的定义域。'e' 是一个常数,具有固定值,所以没有应用极限的理由。
你好,好文章。
1) 在实际的机器学习项目中,洛必达法则真的适用吗?我的意思是,我们通常处理的是数据行而不是解析函数,因此梯度通常是使用迭代方法或外推法计算的。
2) “查看 Mehreen Saeed 的所有文章”的链接似乎已损坏。
祝好运!
您好,感谢您的好文章。不过,我认为正确的拼写应该是“L’Hôpital”,而不是“hospital”…
根据我的法国微积分老师的说法,这两种拼写是等效的,您会在数学文献中看到两者。