微积分的许多领域都需要理解连续函数。连续函数的特征以及对不连续点的研究，都引起了数学界的极大兴趣。由于其重要的性质，连续函数在机器学习算法和优化方法中有着实际应用。
在本教程中，您将了解什么是连续函数、它们的性质，以及优化算法研究中的两个重要定理：介值定理和极值定理。
完成本教程后，您将了解：
- 连续函数的定义
- 介值定理
- 极值定理
让我们开始吧。
连续函数入门 图：Jeeni Khala 拍摄，保留部分权利。
教程概述
本教程分为两部分；它们是：
- 连续函数的定义
- 非正式定义
- 正式定义
- 定理
- 介值定理
- 极值定理
先决条件
本教程需要理解极限的概念。为了帮助您回忆，您可以参考极限与连续，其中也简要介绍了连续函数。在本教程中，我们将深入探讨更多细节。
我们还将使用区间。方括号表示闭区间（包含边界点），圆括号表示开区间（不包含边界点），例如：
- [a,b] 表示 a<=x<=b
- (a,b) 表示 a<x<b
- [a,b) 表示 a<=x<b
从上面的例子可以看出，一个区间可以在一侧是开的，在另一侧是闭的。
最后一点，我们将只讨论定义在实数上的实函数。我们不会讨论复数或定义在复平面上的函数。
连续函数的非正式定义
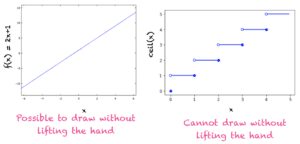
假设我们有一个函数 f(x)。如果我们能在不抬起手的情况下绘制 f(x) 的图形，那么我们就可以轻松地检查它在两个点 a 和 b 之间的连续性。例如，考虑一个定义为
f(x)=2x+1
我们可以在 [0,1] 之间绘制直线而无需抬起手。事实上，我们可以在任何两个 x 值之间绘制这条直线，而无需抬起手（见下图）。因此，该函数在其整个实数定义域上都是连续的。现在让我们看看绘制天花板函数（ceil function）时会发生什么
连续函数（左）和不连续函数（右）
例如，在区间 (0,1] 上，天花板函数的值为 1，ceil(0.5)= 1，ceil(0.7) = 1，依此类推。因此，该函数在定义域 (0,1] 上是连续的。如果我们调整区间为 (0,2]，一旦 x>1，ceil(x) 就会跳到 2。要绘制定义域 (0,2] 的 ceil(x)，我们现在必须抬起手，并在 x=2 处重新开始绘制。因此，天花板函数不是连续函数。
如果函数在其整个实数定义域上都是连续的，那么它就是整体上的连续函数；否则，它就是整体上不连续的。对于后一种函数，我们可以检查它们在哪一个区间上是连续的。
正式定义
如果当 x 趋近于 a 时，函数的值趋近于 f(a)，则函数 f(x) 在点 a 处是连续的。因此，要测试函数在点 x=a 处的连续性，请检查以下条件：
- f(a) 必须存在
- 当 x 趋近于 a 时，f(x) 必须存在极限
- 当 x 趋近于 a 时，f(x) 的极限必须等于 f(a)
如果以上所有条件都成立，则该函数在点 a 处是连续的。
示例
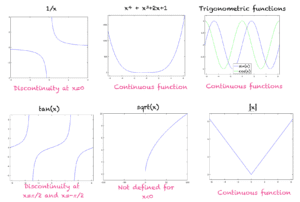
下面列出了一些示例，并在图中进行了展示
- f(x) = 1/x 在 x=0 处不连续，因为它在该点未定义。但是，该函数对于定义域 x>0 是连续的。
- 所有多项式函数都是连续函数。
- 三角函数 sin(x) 和 cos(x) 是连续的，并在 -1 和 1 之间振荡。
- 三角函数 tan(x) 不是连续的，因为它在 x=????/2, x=-????/2 等处未定义。
- sqrt(x) 不是连续的，因为它对于 x<0 未定义。
- |x| 在处处连续。
连续函数和不连续函数的示例
连续性与函数导数的关系
从极限的连续性定义，我们得到一个替代定义。如果 f(x+h)-f(x)→ 0 当 (h→0) 时，则 f(x) 在 x 处连续
f(x+h)-f(x)→ 0 当 (h→0)
让我们看看导数的定义
f'(x) = lim(h→0) (f(x+h)-f(x))/h
因此，如果 f'(x) 在点 a 处存在，则该函数在 a 处是连续的。反之则不一定成立。一个函数可能在点 a 处是连续的，但 f'(a) 不存在。例如，在上图中的 |x| 函数在处处连续。我们可以在不抬起手的情况下绘制它，但是，在 x=0 处，由于曲线的急剧转折，其导数不存在。
介值定理
介值定理指出：
如果
- 函数 f(x) 在 [a,b] 上连续
- 且 f(a) <= K <= f(b)
然后
- 则在 a 和 b 之间存在一个点 c，即 a<=c<=b，使得 f(c) = K
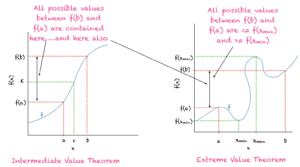
用最简单的话来说，这个定理表明，如果一个函数在 [a,b] 上是连续的，那么该函数在 f(a) 和 f(b) 之间的所有值都将在此区间内存在，如下图所示。
介值定理（左）和极值定理（右）的说明
极值定理
该定理指出：
如果
- 函数 f(x) 在 [a,b] 上连续
然后
- 在区间 [a,b] 内存在点 x_min 和 x_max，即
- a<=x_min<=b
- a<=x_max<=b
- 并且函数 f(x) 有一个最小值 f(x_min) 和一个最大值 f(x_max)，即：
- 当 a<=x<=b 时，f(x_min)<=f(x)<=f(x_max)
简单来说，一个连续函数在区间内总会有一个最小值和一个最大值，如下图所示。
连续函数与优化
连续函数在优化问题的研究中非常重要。我们可以看到，极值定理保证了在区间内，总会存在一个函数取得最大值的点。同样，也可以说存在一个取得最小值的点。许多优化算法都源于这个基本性质，并能执行令人惊叹的任务。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 收敛和发散序列
- 基于无穷小常数的魏尔斯特拉斯和约当连续函数定义
如果您探索了这些扩展内容中的任何一个，我很想知道。请在下面的评论中发布您的发现。
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
教程
资源
- 机器学习微积分书籍 的其他资源
书籍
- 《托马斯微积分》，第14版，2017年。（基于 George B. Thomas 的原创作品，由 Joel Hass, Christopher Heil, Maurice Weir修订）
- 微积分，第三版，2017年。（Gilbert Strang）
- 《微积分》，第8版，2015年。（James Stewart）
总结
在本教程中，您了解了连续函数这一概念。
具体来说，你学到了：
- 什么是连续函数
- 连续函数的正式和非正式定义
- 不连续点
- 介值定理
- 极值定理
- 为什么连续函数很重要
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
这是一篇不错的文章，但是极值定理的图示令人困惑，因为它使得 f(x) 看起来可以产生多个 y 值——也就是说，直线在 x 轴上交叉回去了。