在熟悉了Transformer 模型及其注意力机制的理论之后，我们将首先了解如何实现缩放点积注意力，从而开始我们实现完整 Transformer 模型的旅程。缩放点积注意力是多头注意力的组成部分，而多头注意力又是 Transformer 编码器和解码器的重要组成部分。我们的最终目标是将完整的 Transformer 模型应用于自然语言处理 (NLP)。
在本教程中，您将学习如何在 TensorFlow 和 Keras 中从零开始实现缩放点积注意力。
完成本教程后，您将了解：
- 构成缩放点积注意力机制的操作
- 如何从零开始实现缩放点积注意力机制
通过我的书籍《使用注意力构建 Transformer 模型》启动您的项目。它提供了带有工作代码的自学教程，指导您构建一个可以
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...
让我们开始吧。
如何在 TensorFlow 和 Keras 中从零开始实现缩放点积注意力
图片来源：Sergey Shmidt，保留部分权利。
教程概述
本教程分为三个部分；它们是：
- Transformer 架构回顾
- Transformer 缩放点积注意力
- 从零开始实现缩放点积注意力
- 测试代码
先决条件
本教程假设您已熟悉以下内容：
Transformer 架构回顾
回顾我们已经看到 Transformer 架构遵循编码器-解码器结构。左侧的编码器负责将输入序列映射到连续表示序列；右侧的解码器接收编码器的输出以及解码器在上一时间步的输出来生成输出序列。
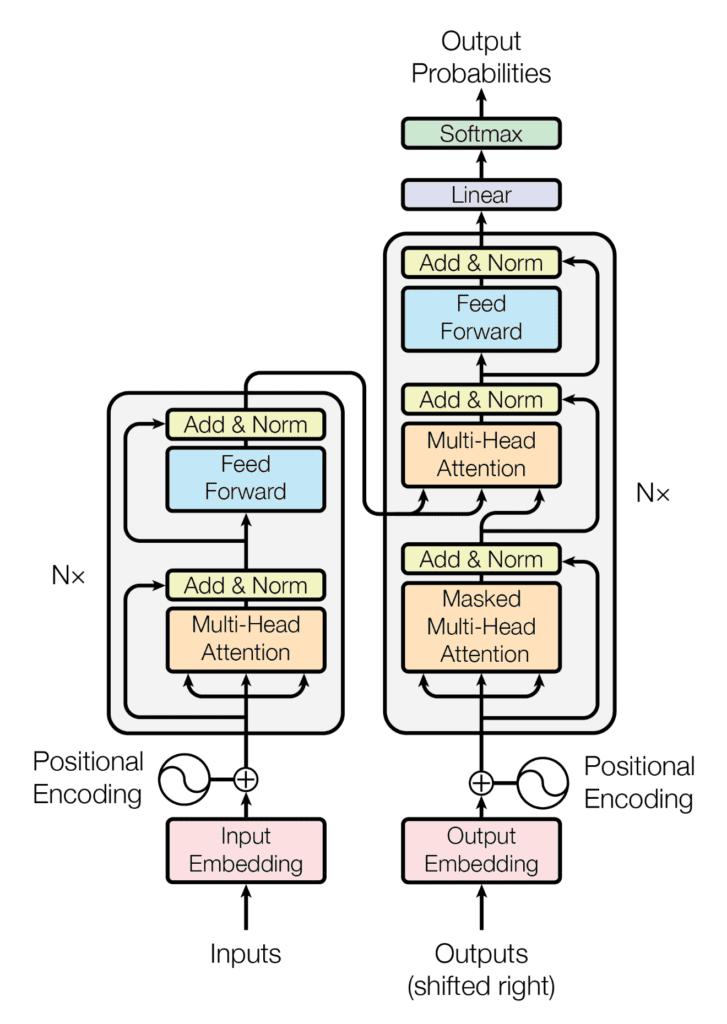
Transformer 架构的编码器-解码器结构
摘自“Attention Is All You Need”
在生成输出序列时，Transformer 不依赖于循环和卷积。
您已经看到 Transformer 的解码器部分在架构上与编码器有许多相似之处。编码器和解码器在其多头注意力块中共享的核心组件之一是缩放点积注意力。
Transformer 缩放点积注意力
首先，回顾查询、键和值是您将要处理的重要组件。
在编码器阶段，它们在嵌入并添加位置信息后都携带相同的输入序列。同样，在解码器端，馈入第一个注意力块的查询、键和值代表相同的目标序列，该序列也已嵌入并添加位置信息。解码器的第二个注意力块以键和值的形式接收编码器输出，并以查询的形式接收第一个注意力块的归一化输出。查询和键的维度表示为 $d_k$，而值的维度表示为 $d_v$。
缩放点积注意力接收这些查询、键和值作为输入，并首先计算查询与键的点积。结果随后通过 $d_k$ 的平方根进行缩放，从而产生注意力分数。然后将它们输入到 softmax 函数中，获得一组注意力权重。最后，注意力权重用于通过加权乘法运算来缩放值。整个过程可以用数学表示如下，其中 $\mathbf{Q}$、$\mathbf{K}$ 和 $\mathbf{V}$ 分别表示查询、键和值
$$\text{attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax} \left( \frac{\mathbf{Q} \mathbf{K}^\mathsf{T}}{\sqrt{d_k}} \right) \mathbf{V}$$
Transformer 模型中的每个多头注意力块都实现了一个缩放点积注意力操作，如下所示
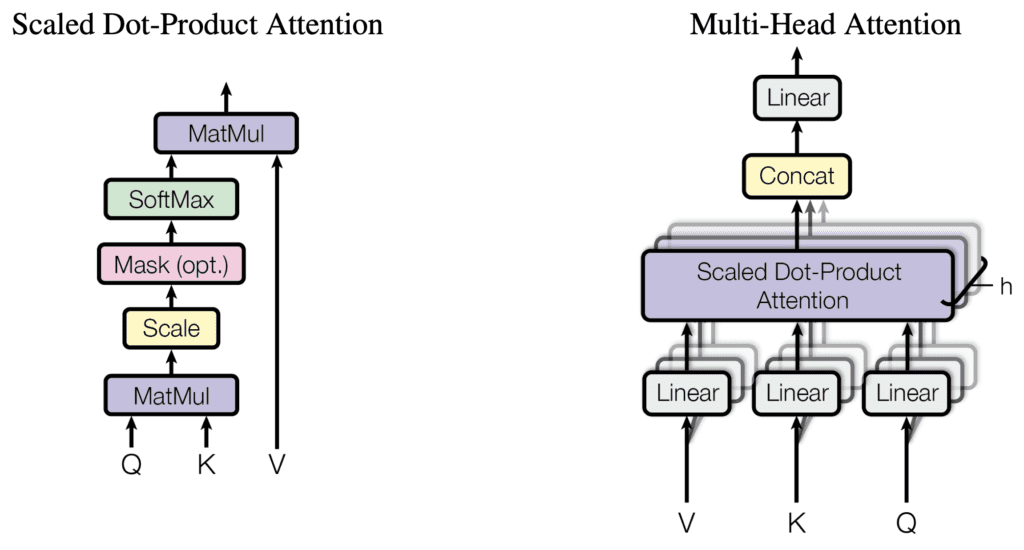
缩放点积注意力和多头注意力
摘自“Attention Is All You Need”
您可能会注意到，缩放点积注意力也可以在将注意力分数输入 softmax 函数之前应用掩码。
由于词嵌入被零填充到特定的序列长度，因此需要引入填充掩码，以防止零标记与编码器和解码器阶段的输入一起处理。此外，还需要前瞻掩码以防止解码器关注后续单词，使得对特定单词的预测只能依赖于其之前单词的已知输出。
这些前瞻掩码和填充掩码应用于缩放点积注意力内部，将 softmax 函数输入中所有不应考虑的值设置为 -$\infty$。对于这些较大的负输入中的每一个，softmax 函数将依次产生接近零的输出值，从而有效地将其屏蔽掉。当您在单独的教程中逐步实现编码器和解码器块时，这些掩码的使用将变得更加清晰。
目前，让我们看看如何在 TensorFlow 和 Keras 中从零开始实现缩放点积注意力。
想开始构建带有注意力的 Transformer 模型吗？
立即参加我的免费12天电子邮件速成课程（含示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
从零开始实现缩放点积注意力
为此，您将创建一个名为 DotProductAttention 的类，该类继承自 Keras 中的 Layer 基类。
在此类中，您将创建一个类方法 call()，该方法将查询、键和值以及维度 $d_k$ 和一个掩码（默认为 None）作为输入参数
|
1 2 3 4 5 6 |
class DotProductAttention(Layer): def __init__(self, **kwargs): super(DotProductAttention, self).__init__(**kwargs) def call(self, queries, keys, values, d_k, mask=None): ... |
第一步是在查询和键之间执行点积操作，并对后者进行转置。结果将通过除以 $d_k$ 的平方根进行缩放。您将向 call() 类方法添加以下代码行
|
1 2 3 |
... scores = matmul(queries, keys, transpose_b=True) / sqrt(d_k) ... |
接下来，您将检查 mask 参数是否已设置为非默认值 None。
掩码将包含 0 值以表示应在计算中考虑输入序列中的相应标记，或包含 1 以表示不应考虑。掩码将乘以 -1e9 以将 1 值设置为大的负数（记住前面提到过这一点），然后应用于注意力分数
|
1 2 3 4 |
... if mask is not None: scores += -1e9 * mask ... |
然后注意力分数将通过 softmax 函数生成注意力权重
|
1 2 3 |
... weights = softmax(scores) ... |
最后一步是通过另一个点积操作，用计算出的注意力权重对值进行加权
|
1 2 |
... return matmul(weights, values) |
完整的代码清单如下
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from tensorflow import matmul, math, cast, float32 from tensorflow.keras.layers import Layer from keras.backend import softmax # 实现缩放点积注意力 class DotProductAttention(Layer): def __init__(self, **kwargs): super(DotProductAttention, self).__init__(**kwargs) def call(self, queries, keys, values, d_k, mask=None): # 在转置键后对查询进行评分，并进行缩放 scores = matmul(queries, keys, transpose_b=True) / math.sqrt(cast(d_k, float32)) # 将掩码应用于注意力分数 if mask is not None: scores += -1e9 * mask # 通过 softmax 操作计算权重 weights = softmax(scores) # 通过值向量的加权和计算注意力 return matmul(weights, values) |
测试代码
您将使用 Vaswani 等人 (2017) 的论文《Attention Is All You Need》中指定的参数值
|
1 2 3 4 |
d_k = 64 # 线性投影查询和键的维度 d_v = 64 # 线性投影值的维度 batch_size = 64 # 训练过程中的批处理大小 ... |
至于序列长度以及查询、键和值，您目前将使用虚拟数据，直到您在单独的教程中训练完整的 Transformer 模型的阶段，届时您将使用实际句子。同样，对于掩码，暂时将其设置为默认值
|
1 2 3 4 5 6 7 |
... input_seq_length = 5 # 输入序列的最大长度 queries = random.random((batch_size, input_seq_length, d_k)) keys = random.random((batch_size, input_seq_length, d_k)) values = random.random((batch_size, input_seq_length, d_v)) ... |
在完整的 Transformer 模型中，序列长度以及查询、键和值将通过词元化和嵌入过程获得。您将在单独的教程中介绍这一点。
回到测试过程，下一步是创建 DotProductAttention 类的新实例，将其输出分配给 attention 变量
|
1 2 3 |
... attention = DotProductAttention() ... |
由于 DotProductAttention 类继承自 Layer 基类，因此前者的 call() 方法将由后者的魔法 __call()__ 方法自动调用。最后一步是输入参数并打印结果
|
1 2 |
... print(attention(queries, keys, values, d_k)) |
将所有内容结合起来，生成以下代码清单
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from numpy import random input_seq_length = 5 # 输入序列的最大长度 d_k = 64 # 线性投影查询和键的维度 d_v = 64 # 线性投影值的维度 batch_size = 64 # 训练过程中的批处理大小 queries = random.random((batch_size, input_seq_length, d_k)) keys = random.random((batch_size, input_seq_length, d_k)) values = random.random((batch_size, input_seq_length, d_v)) attention = DotProductAttention() print(attention(queries, keys, values, d_k)) |
运行此代码会产生形状为（批处理大小，序列长度，值维度）的输出。请注意，由于查询、键和值的随机初始化，您可能会看到不同的输出。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
tf.Tensor( [[[0.60413814 0.52436507 0.46551135 ... 0.5260341 0.33879933 0.43999898] [0.60433316 0.52383804 0.465411 ... 0.5262608 0.33915892 0.43782598] [0.62321603 0.5349194 0.46824688 ... 0.531323 0.34432083 0.43554053] [0.60013235 0.54162943 0.47391182 ... 0.53600514 0.33722004 0.4192218 ] [0.6295709 0.53511244 0.46552944 ... 0.5317217 0.3462567 0.43129003]] ... [[0.20291057 0.18463902 0.641182 ... 0.4706118 0.4194418 0.39908117] [0.19932748 0.18717204 0.64831126 ... 0.48373622 0.3995132 0.37968236] [0.20611541 0.18079443 0.6374859 ... 0.48258874 0.41704425 0.4016996 ] [0.19703123 0.18210654 0.6400498 ... 0.47037745 0.4257752 0.3962079 ] [0.19237372 0.18474475 0.64944196 ... 0.49497223 0.38804317 0.36352912]]], shape=(64, 5, 64), dtype=float32) |
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
书籍
- 使用 Python 进行高级深度学习, 2019
- 用于自然语言处理的 Transformer, 2021
论文
- 注意力就是你所需要的一切, 2017
总结
在本教程中，您学习了如何在 TensorFlow 和 Keras 中从零开始实现缩放点积注意力。
具体来说，你学到了：
- 构成缩放点积注意力机制的操作
- 如何从零开始实现缩放点积注意力机制
你有什么问题吗？
在下面的评论中提出您的问题，我将尽力回答。
学习 Transformer 和注意力！
教您的深度学习模型阅读句子
...使用带有注意力的 Transformer 模型
在我的新电子书中探索如何实现
使用注意力机制构建 Transformer 模型
它提供了自学教程和可运行代码，指导您构建一个可以
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...
TypeError: DotProductAttention.__init__() 接受 1 个位置参数，但给出了 5 个。
我收到此错误。相反，我必须调用 attention.cal(….)。有什么解决办法吗？
您必须导入“from dumpy import random”
*numpy
您好，感谢这篇精彩的文章！感谢您花时间添加测试函数的参数，我认为如果您在 Q、K、V 的随机生成之前添加随机种子，测试会更有用。
例如，在生成三个随机向量之前调用 random.seed(42)，我得到以下输出
[[[0.42829984 0.5291363 0.48467717 … 0.60236526 0.6314437 0.36796492]
[0.42059597 0.51898783 0.46809804 … 0.59751767 0.63140476 0.39604473]
[0.45291767 0.53372955 0.4822161 … 0.5861658 0.61705434 0.35611778]
[0.43538865 0.52972203 0.47826144 … 0.5917443 0.6259302 0.36665624]
[0.42998832 0.5189111 0.48113108 … 0.61032706 0.63044846 0.39192218]]
[[0.6105153 0.50249505 0.40130395 … 0.71487725 0.36341453 0.5512418 ]
[0.58420086 0.5239525 0.4311911 … 0.72335523 0.36001056 0.5697574 ]
[0.5644941 0.5598139 0.44120124 … 0.69758904 0.34060007 0.57147545]
[0.58783877 0.5212065 0.42275837 … 0.70439875 0.34812242 0.5561169 ]
[0.5880349 0.52016133 0.43390357 … 0.70503277 0.35547623 0.56170976]
感谢您的反馈和建议 Giovanni！
缩放点积注意力的输出是什么意思？
R =softmax(scale( ( Q @K.T ) ) @ V
这个 R 矩阵代表什么？
嗨，Inquisitive……缩放点积注意力机制的输出矩阵 \( R \) 代表值向量 \( V \) 的注意力加权和。以下是对公式中每个步骤的详细解释以及最终 \( R \) 矩阵的表示
### 缩放点积注意力的组成部分
1. **查询 (Q)**
– 包含查询的矩阵。每个查询向量对应一个输入标记，用于确定应向每个键付出多少注意力。
2. **键 (K)**
– 包含键的矩阵。每个键向量对应一个输入标记，用于与查询匹配以计算注意力分数。
3. **值 (V)**
– 包含值的矩阵。每个值向量对应一个输入标记，并根据注意力分数保存应聚合的信息。
### 缩放点积注意力的步骤
1. **Q 和 \( K^T \) 的点积**
– 查询矩阵 \( Q \) 和键矩阵 \( K \) 的转置的点积产生一个原始注意力分数矩阵。
\[
\text{raw\_scores} = Q \cdot K^T
\]
每个元素 \( \text{raw\_scores}_{ij} \) 表示第 \( i \) 个查询和第 \( j \) 个键之间的注意力分数。
2. **缩放**
– 原始注意力分数通过键向量维度 \( \sqrt{d_k} \) 的平方根进行缩放。这有助于稳定训练期间的梯度并防止 softmax 变得过于平坦或过于尖锐。
\[
\text{scaled\_scores} = \frac{Q \cdot K^T}{\sqrt{d_k}}
\]
3. **Softmax**
– 缩放后的分数通过 softmax 函数以获得注意力权重。这将分数转换为每个查询的总和为 1 的概率。
\[
\text{attention\_weights} = \text{softmax}\left(\frac{Q \cdot K^T}{\sqrt{d_k}}\right)
\]
每个元素 \( \text{attention\_weights}_{ij} \) 表示第 \( i \) 个查询和第 \( j \) 个键之间的归一化注意力分数。
4. **与 V 的加权和**
– 注意力权重用于计算值向量 \( V \) 的加权和。这会产生最终的输出矩阵 \( R \)。
\[
R = \text{attention\_weights} \cdot V
\]
\( R \) 的每一行都是所有值向量的加权和，其中权重由对应查询的注意力分数给出。
### \( R \) 的解释
矩阵 \( R \) 代表注意力输出。具体而言
– \( R \) 中的每一行对应于特定查询的注意力输出。
– 注意力机制允许每个查询关注输入序列的不同部分（由键和值表示），并以加权方式聚合这些部分的信息。
– \( R \) 捕获了输入序列中最相关的信息，由注意力机制确定。
总之，\( R \) 是注意力加权值矩阵，其中每个输出向量（\( R \) 中的行）是一个上下文向量，它以与相应查询相关的方式总结了输入序列。这使得模型能够针对不同的查询动态地关注输入的不同部分，从而增强其理解和处理输入数据的能力。